Consistent Hashing

Consistent Hashing isn’t just a buzzword 🫠, it’s the secret sauce behind the magic of distributed computing. Imagine a world where your data effortlessly flows across a dynamic network of servers 📺, adapting seamlessly to scale and resilience. That’s the promise of Consistent Hashing, the elegant technique that keeps modern systems cool, efficient, and ready for whatever challenges the digital cosmos throws their way.

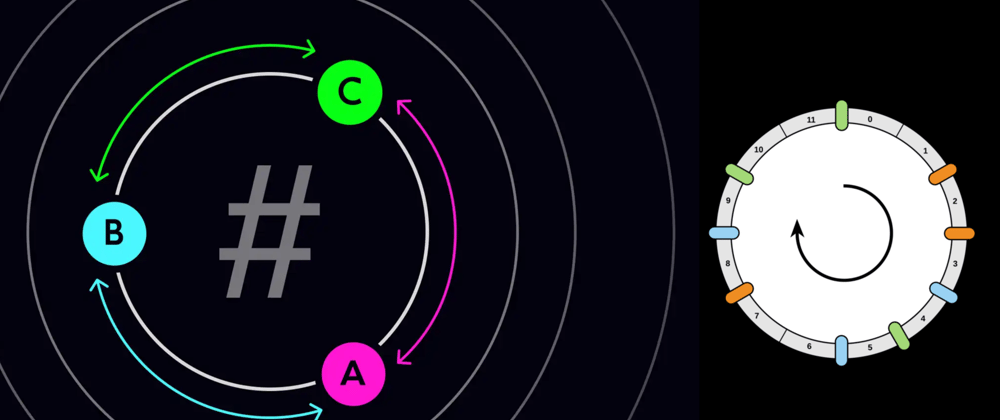
Picture a cosmic ring, where data and nodes dance together. With a twist of the hash function, data finds its perfect partner on this celestial ring, ensuring even load distribution and zero hotspots. But here’s where it gets cool: when a new server joins the party or an old one takes its leave, only a fraction of data needs to groove to a new beat, keeping disruption to a minimum.

So, let’s dive deeply 👇

Why do we need a hashing function????

Ohk so let’s start with very basic if you want to map N no of keys how will you do that ?. One of the very basic approach will be like this 👇

But the problem with this approach is that if we have a very big number of possible keys this approach will lead to a lot of Memory wastage.

We can fix this by using a hashing algorithm or a hashing function whatever you want to call it.

Hash functions are efficient because they need less memory and have fast lookup and insertion times, averaging O(1) complexity. They turn large or variable-sized inputs into a fixed-size output, making them space-efficient compared to direct address tables that need space for the entire range of possible keys. While worst-case time complexity can worsen, especially if many collisions occur, proper design keeps operations swift and memory use proportional to the actual number of entries, generally O(n).

First let’s understand what normal hashing or called as static or modular hashing is suppose you have n servers and N no of keys so you will have [n-1] buckets the mapping of keys is done with a hashing function which will return index from 0 to n-1.

# modular hashing
hash = key % N of nodes

But here’s the kicker: It’s like a game of musical chairs. When you remove a chair (server), everyone has to find a new seat, and it’s a hot mess. As the cluster size grows, this becomes unsustainable because the amount of work required for each hash change grows linearly with cluster size.

Consistent Hashing, on the other hand, introduces the concept of a virtual ring. It doesn’t really care if servers come and go. It’s like having an elastic waistband on Thanksgiving—you can add or remove without a full wardrobe malfunction.

Consistent hashing is a distributed hashing scheme that operates independently of the number of servers or objects in a distributed hash table by assigning them a position on an abstract circle, or hash ring. The main advantage of consistent hashing is that when a server is added or removed, only a small proportion of keys need to be remapped, which is important for distributed systems, like databases, caches, and load balancers, where minimizing reshuffling is beneficial.

You can consider them as the users which are requesting some data from a servers and lets suppose we have N servers, A, B ,C… and The servers are hashed onto the ring using H(x), placing each server at a point on the circle.

Every Request from user will be handled by the server next to it we can move clockwise or anticlockwise doesn’t matter.

Adding a Server

When a new server is added to a consistent hashing ring, the keys that are now closer to the new server’s hash value will be reassigned to it. Here’s the math behind it:

• Calculate the hash of the new server, let’s call it H(new_server).
• Find the location on the ring where H(new_server) falls.
• Any keys that fall between H(new_server) and the next server on the ring in a clockwise direction will be reassigned to new_server.

The number of keys that need to be reassigned depends on the distribution of the keys and the position of the new server on the ring. If the keys are evenly distributed, the number of keys that need to be moved is approximately K/N, where K is the total number of keys and N is the total number of servers after adding the new server.

Removing a Server

When a server needs to be removed, a similar but reverse process occurs:

• Calculate the hash of the server to be removed, H(removed_server).
• Find the server’s location on the ring.
• Reassign all keys that were assigned to removed_server to the next server on the ring in a clockwise direction.

Again, if keys are evenly distributed, the number of keys that need to be moved is approximately K/N, where K is the total number of keys and N is the total number of servers after removing the server.

To achieve a balanced key distribution among servers, we implement a clever technique: we give multiple identifiers (angles) to each server on the hash circle. Instead of single identifiers like A, B, and C, we would use a series of identifiers for each A0 through A9, B0 through B9, C0 through C9 spaced out around the circle. The number of identifiers per server, which we call the ‘weight’, can vary based on the server’s capacity and the specific requirements of the system. If, for example, server B is twice as capable as the others, it would receive double the identifiers, thereby statistically handling twice the number of objects.

Let’s break it down. Your keys do a little hash dance and land on a spot on the ring. When you add a new server, it just squeezes in, causing minimal movement of those keys—they just scoot over a bit.

Connect me on Twitter :- Twitter 🤝🏻

Do check out my Github for amazing projects:- Github 🤝🏻

Connect me on LinkedIn :- Linkedin 🤝🏻